Convolutional neural network (CNN) has been widely used in sequence classification and mechanism mining of omic datasets since the publication of the two pilot studies, DeepBind (1) and DeepSEA (2). The intrinsic operation of CNN itself, however, has long been taken as a ‘black-box’. Recently some studies have attempted to tackle this problem; for example, SpliceRover (3) visualizes learnt CNN signals with DeepLIFT (6); these studies, however, focused mainly on heuristically estimating the effect of change in input on the activation of neurons, and did not interpret the operation of CNN precisely.
We noted that the core operation in CNN models, scanning with convolutional kernels, is essentially a one-dimensional window scanning where the kernel has an important property related to Position Weight Matrix (PWM): with the input sequence one hot-encoded (Fig. 1A), the convolution score is exactly the log-likelihood if the kernel is exactly the logarithm of the position-specific probabilities (Fig. 1B). More generally, if the kernel is the log odds ratios of these probabilities to the background distribution (which is the way most PWM’s are defined), then the convolution score is exactly the logarithm of Bayesian factor describing whether the sequence fragment resembles the true signal more than random sequences (Fig. 1C). This relationship has been pinpointed by Prof. Ming-Hua Deng during his course Statistical models in bioinformatics.
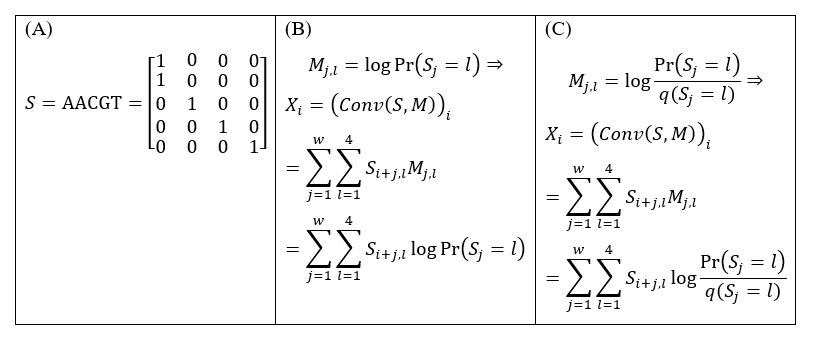
Figure 1. When the kernel is exactly the PWM itself, its convolution score is exactly the log-likelihood (or the logarithm of Bayesian factor) of the PWM. (A) Sequence S in one hot-encoding. (B) If the kernel M is the logarithm of the position-specific probabilities of a PWM, then the convolution score of M with S at position i, Xi, is equal to the log-likelihood of this PWM at the same position of S. (C) If the kernel is the log odds ratios of the position-specific probabilities to the background probabilities described by the PWM, then Xi is the Bayesian factor of this PWM at the same position of S.
At the same time, Dr. Yang Ding developed the equivalence between an arbitrary kernel and the log-likelihood of PWM (7) (Fig. 2A): the convolution score of a given kernel on a given sequence is exactly a constant plus “the log-likelihood of a PWM explicitly transformed from the kernel (Fig. 2B) on the same sequence”. Compared with Deng’s interpretation (Fig. 1), Ding’s interpretation does not require the kernel elements to be logarithm of probabilities or odds ratios, thus enabling its application to arbitrary CNN models with input sequence one hot-encoded.
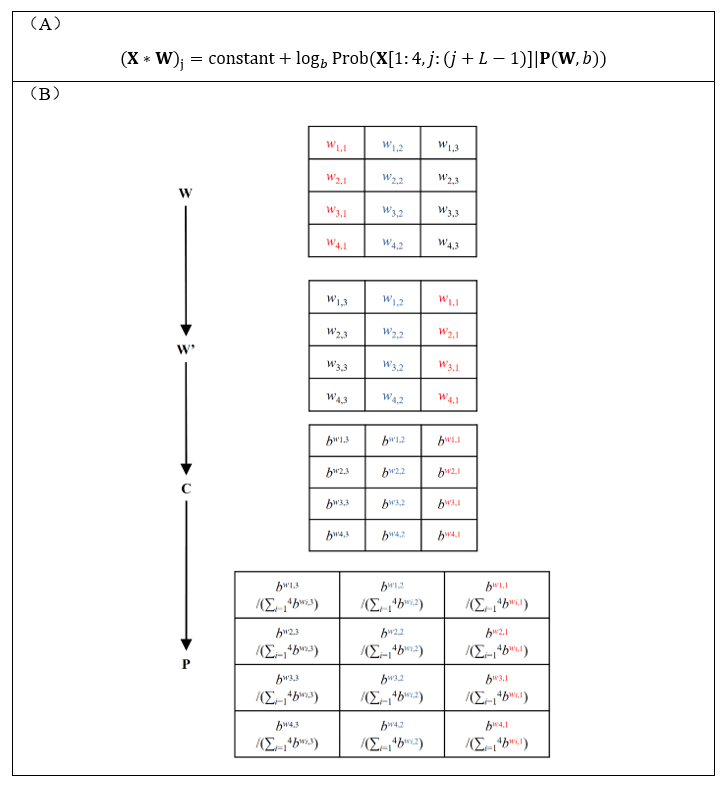
Figure 2. Any arbitrary kernel of a CNN model is equivalent to a PWM. (A) For any arbitrary sequence X and kernel W, the convolution score is equal to the sum of a constant and “the log-likelihood of a PWM explicitly transformed from the kernel on the same sequence”. (B) The pipeline describing how the PWM P can be explicitly transformed from the kernel W. The b is a constant larger than 1.
Inspired by the quantitative probabilistic interpretation for kernels and the classical EM algorithm adopted by motif finding studies in 1990s (8), we designed a novel pooling layer, the Expectation Pooling (or “ePooling” in short), to replace the commonly used global max-pooling (Fig. 3A, Fig. 3B). The concept of “expectation pooling” stems naturally from the E-step of the EM algorithm, and can also be regarded statistically a “soft” variant of global max-pooling, i.e., it computes the “soft” maximum of convolution scores. Based on the equivalence between arbitrary kernels and PWMs above (7), we proved that the output of ePooling is (up to a constant difference) exactly the expected log-likelihood of the corresponding PWM, which is also the output of E-step in the EM algorithm (Fig. 3C).
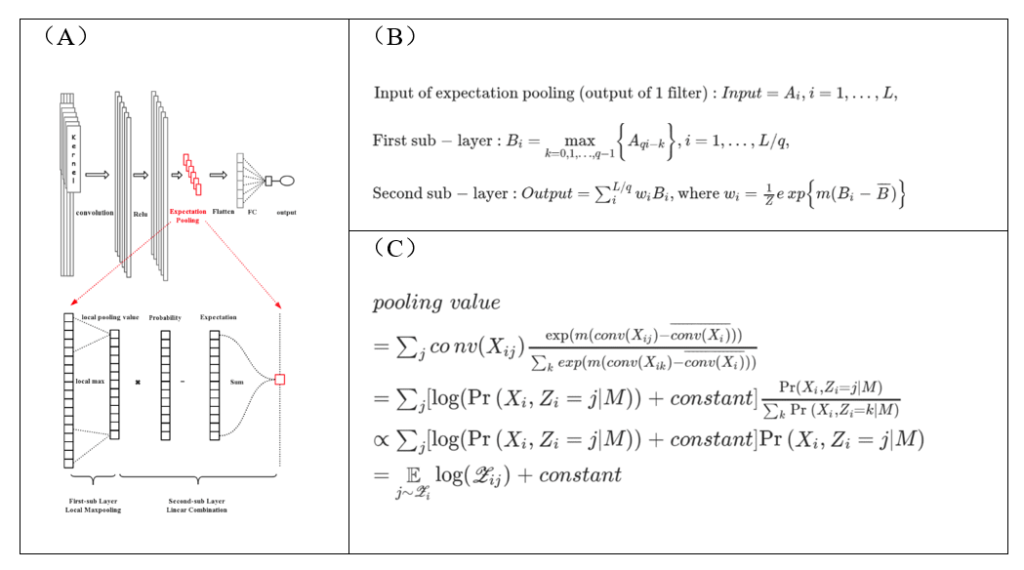
Figure 3. Expectation pooling (ePooling) has a straightforward and precise interpretation. (A) The overall design of ePooling. (B) Equations describing how ePooling computes. (C) The output of ePooling is (up to a constant difference) exactly the log-likelihood of the corresponding PWM.
Simulation showed that models equipped with ePooling have a better AUC and robustness (Fig. 4A) than those with traditional max pooling or average pooling, and are also less overfitted than those with max pooling (Fig. 4B). In addition, replacing max pooling with ePooling helps to improve model’s AUC on most datasets, as demonstrated by a benchmark on 690 real ChIP-Seq datasets (Table 1).
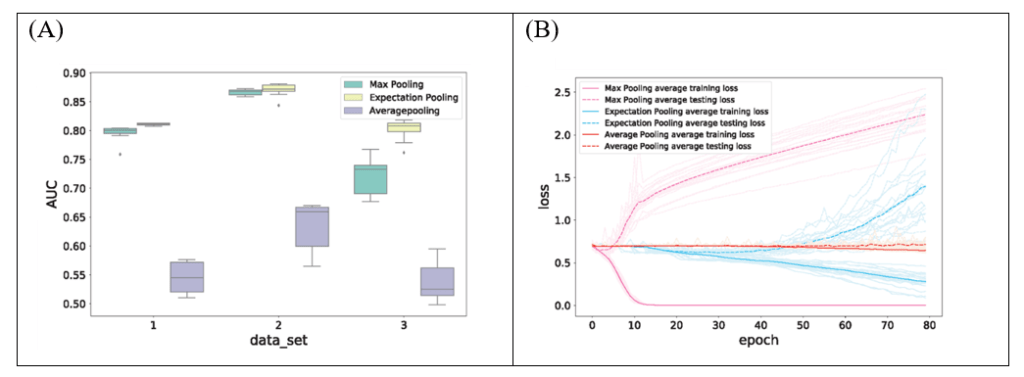
Figure 4. The ePooling layer performs well on simulated datasets. (A) The ePooling layer helps the model to obtain a better AUC and robustness compared with traditional max pooling and average pooling. (B) Replacing max pooling with ePooling can reduce overfitting effectively.
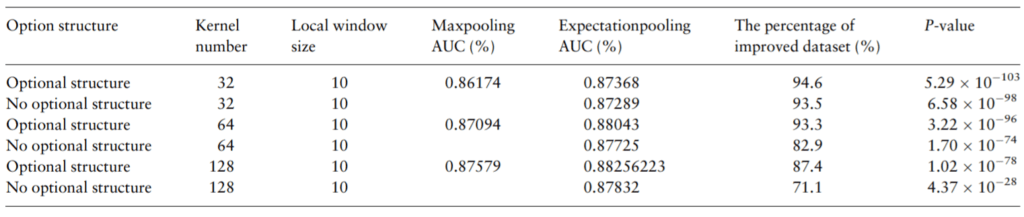
Table 1. Replacing traditional max pooling with ePooling helps to improve CNN’s AUC on most datasets, as demonstrated by the benchmark on 690 real ChIP-Seq datsets.
CNN plays a more and more critical role in bioinformatics and omics studies nowadays. Following a rational design, ePooling improves the mainstream pooling layers in the sense of probabilistic interpretability. It not only improves model performance, but also helps researchers to better understand the underlying biological sequence patterns from a statistical view, and presents some intriguing probabilistic ideas. We believe that the integration of statistical learning with deep learning helps to ‘transparentize’ the ‘black-box’, i.e., to develop deep learning models that are more and more interpretable, which could help researchers to discover more complex biological mechanisms.
This work was done in cooperation with Prof. Ming-Hua Deng’s lab at School of Mathematical Sciences and Center for Quantitative Biology, Peking University, and was published online by Bioinformatics on October 9th, 2019 with the title ‘Expectation pooling: an effective and interpretable pooling method for predicting DNA–protein binding’. Ph.D. candidate Xiao Luo (from School of Mathematical Sciences, Peking University) and undergraduate Xin-Ming Tu (from School of Life Sciences, Peking University) are the co-first authors of this work, and Prof. Ming-Hua Deng and Dr. Ge Gao are the correspondence authors. Dr. Yang Ding provided substantial help on discussion of preliminary ideas and manuscript revision.
Link to full-text of this work: https://academic.oup.com/bioinformatics/advance-article/doi/10.1093/bioinformatics/btz768/5584233
Codes for this work: https://github.com/gao-lab/ePooling
Reference:
- Alipanahi B, Delong A, Weirauch MT, Frey BJ. Predicting the sequence specificities of DNA- and RNA-binding proteins by deep learning. Nat Biotechnol. 2015 Aug;33(8):831–8.
- Zhou J, Troyanskaya OG. Predicting effects of noncoding variants with deep learning–based sequence model. Nat Methods. 2015 Oct;12(10):931–4.
- Zuallaert J, Godin F, Kim M, Soete A, Saeys Y, De Neve W. SpliceRover: interpretable convolutional neural networks for improved splice site prediction. Hancock J, editor. Bioinformatics. 2018 Dec 15;34(24):4180–8.
- Kelley DR, Snoek J, Rinn JL. Basset: learning the regulatory code of the accessible genome with deep convolutional neural networks. Genome Res. 2016 Jul;26(7):990–9.
- Ben-Bassat I, Chor B, Orenstein Y. A deep neural network approach for learning intrinsic protein-RNA binding preferences. Bioinformatics. 2018 Sep 1;34(17):i638–46.
- Shrikumar A, Greenside P, Kundaje A. Learning Important Features Through Propagating Activation Differences. ArXiv170402685 Cs [Internet]. 2019 Oct 12 [cited 2019 Dec 5]; Available from: http://arxiv.org/abs/1704.02685
- Ding Y, Li J-Y, Wang M, Tu X, Gao G. An exact transformation for CNN kernel enables accurate sequence motif identification and leads to a potentially full probabilistic interpretation of CNN [Internet]. Bioinformatics; 2017 Jul [cited 2019 Dec 5]. Available from: http://biorxiv.org/lookup/doi/10.1101/163220
- Lawrence CE, Reilly AA. An expectation maximization (EM) algorithm for the identification and characterization of common sites in unaligned biopolymer sequences. Proteins Struct Funct Genet. 1990;7(1):41–51.
- Luo X, Tu X, Ding Y, Gao G, Deng M. Expectation pooling: an effective and interpretable pooling method for predicting DNA–protein binding. Hancock J, editor. Bioinformatics. 2019 Oct 9;btz768.